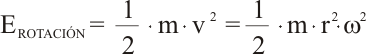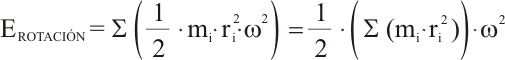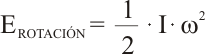Unidades
Trabajo de una fuerza
Trabajo de rotación
Trabajo de un gas
|
TRABAJO DE ROTACIÓN
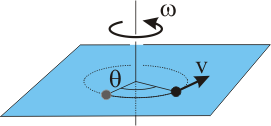
El movimiento de rotación de una partícula se realiza cuando ésta describe circunferencias de radio r alrededor de un eje de giro. Al ángulo girado se le representa con la letra griega θ y se mide en radianes; la velocidad de rotación o velocidad angular se representa con ω y se mide en radianes/segundo.
 |
La relación entre las magnitudes angulares y las del movimiento lineal son sencillas si recordamos la expresión de la longitud de la circunferencia (l = 2 · π · r)
distancia = ángulo · radio
d = θ · r
v = ω · r |
|
Con estas expresiones, la energía cinética de rotación de una partícula se expresa como:
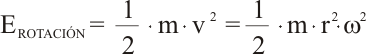
Cuando se trata de un sólido con muchas partículas, la energía de rotación del sólido es la suma de todas las energías de cada una de las partículas o trozos que lo componen:
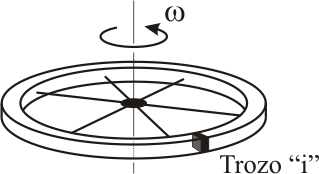 |
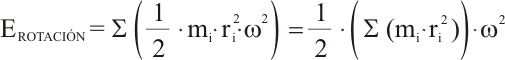
La expresión Σ mi · ri2 se denomina momento de inercia, y de forma análoga a la masa (o masa de inercia), mide la dificultad que tiene un objeto a ponerse en movimiento de rotación respecto a un eje de giro. Pulsando aquí hay algunos momentos de inercia básicos.
Con ésto, la energía de rotación viene dada por la siguiente expresión: |
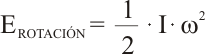
Al igual que una fuerza realiza trabajo cuando produce un desplazamiento, en la mecánica de rotación se realiza un trabajo cuando se produce un giro por efecto de una fuerza.
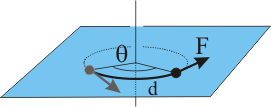 |
El trabajo de la fuerza F viene dado por la expresión:
W = F · d
y, como la distancia recorrida es:
d = θ · r
Se obtiene como trabajo de rotación:
W = F · θ · r
|
Y, por fín, al producto de la fuerza por la distancia del punto de aplicación de ésta al eje de giro mide la capacidad de producir un giro de esa fuerza, y se denomina par o momento de la fuerza, con lo cual, la expresión del trabajo de rotación queda como:
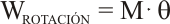
y la potencia de rotación es la velocidad con que se produce un trabajo de rotación, ésto es, el resultado de dividir el trabajo entre el tiempo:

Con todo ésto, la equivalencia entre magnitudes del movimiento lineal y del movimiento de rotación es la siguiente:
| |
Lineal |
Angular |
Relación |
| Desplazamiento |
Distancia (d) |
Ángulo (θ) |
d = θ · r |
| Velocidad |
Velocidad lineal (v) |
Velocidad angular ( ω) |
v = ω · r |
| Inercia |
Masa (m) |
Momento de inercia (I) |
|
| Causa del movimiento |
Fuerza (F) |
Par o Momento (M) |
M = F · r |
| Energía |
Energía cinética ( EC = 1/2 · m · v2 ) |
Energía de rotación ( EROT = 1/2 · I · ω2 ) |
|
| Trabajo |
Trabajo de una fuerza (W = F · d ) |
Trabajo de un momento ( W = M · θ ) |
|
| Potencia |
Velocidad de desplazar fuerza (P = F · v) |
Velocidad de girar momento (P = M · ω) |
|