|
Fuerza de Lorentz |
FUERZA DE LORENTZ Siguiendo con el estudio de la fuerza entre dos cables conductores, Ampère observó que la fuerza de atracción o repulsión era máxima cuando el segundo conductor era perpendicular al plano de los círculos del campo magnético. Al inclinar el cable, la fuerza se reducía con una variación senoidal hasta hacerse nula cuando el ángulo es cero:
|
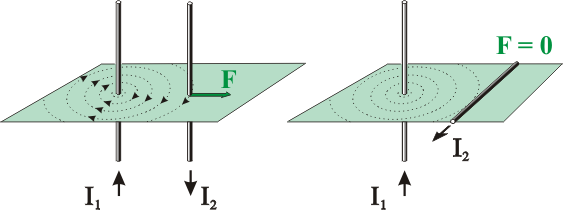
La conclusión es clara: la expresión de la fuerza está afectada por el seno del ángulo que forma la intensidad con el vector campo magnético:
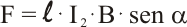
expresión que se puede escribir como un producto vectorial de los vectores I y B:
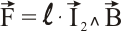
Pero para obtener el sentido correcto del vector F hay que tener en cuenta invertir la intensidad como consecuencia de que es una circulación de cargas negativas.
De forma similar, cuando hay una carga moviéndose en el seno de un campo magnético, aparece sobre ella una fuerza, conocida como fuerza de Lorentz. A partir de la expresión anterior, y teniendo en cuenta que I=q/t y que l/t=v, se obtiene la expresión de esta fuerza de Lorentz:
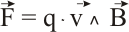
En el siguiente gráfico se puede comprobar la dirección y sentido de la fuerza sobre una carga positiva. Sobre una carga negativa hay que tener en cuenta que el signo negativo de la misma invierte el sentido del vector fuerza:
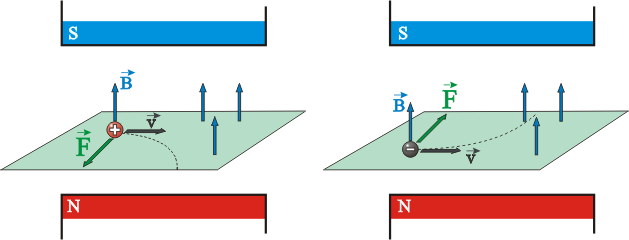
Esta fuerza se puede aprovechar para producir movimiento y, por ende, constituye el principio de los motores eléctricos. Ya sabemos de cursos anteriores que en el interior del motor hay uno o varios campos magnéticos, y una serie de conductores eléctricos formando espiras. Estudiando lo que pasa en una única espira dentro de un campo:
 |
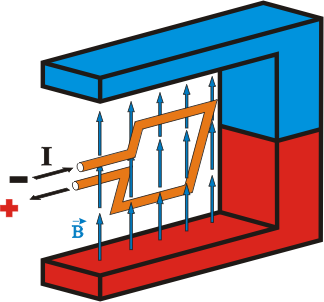Aplicando la expresión de la fuerza sobre un conductor a los cables superior e inferior de la espira tendremos un par de fuerzas:
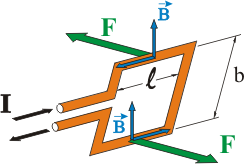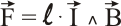
que ejercen un momento de giro sobre la espira. El valor de este momento viene dado por el producto de la fuerza por la distancia que separa ambas líneas de acción: |
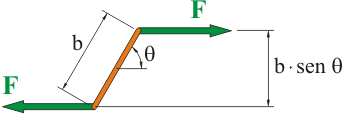
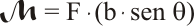
A continuación, se sustituye la fuerza por su valor, teniendo en cuenta que la intensidad y el campo magnético son siempre perpendiculares. Después se reorganizan los términos de la expresión:
Ahora, el producto de la longitud de la espira por su anchura da como resultado la superficie de la misma. Con ésto se obtiene una expresión que es independiente de la forma de la espira, y sólo influye su superficie:
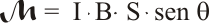
Y, ya para acabar, se transforma esta igualdad en un producto vectorial si se considera la superficie como un vector cuyo módulo es el valor de superficie, dirección perpendicular al plano de la espira y sentido definido por la regla de la mano derecha según el sentido de la intensidad, previamente invertida:
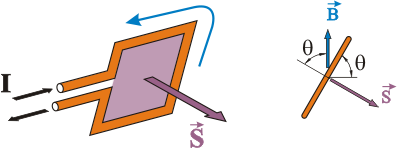
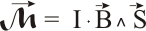
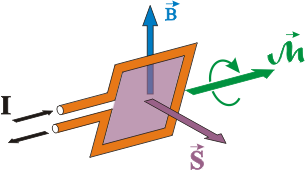
Con lo cual, además, tenemos la dirección del momento de giro como un vector, y nuevamente por la regla de la mano derecha este vector indica el sentido de giro. Cuando hay varias espiras, la expresión se multiplica por el número de las mismas:
 |
 |
 |
 |
