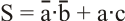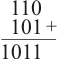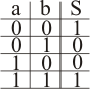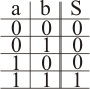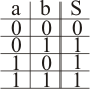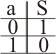Sistemas de numeración Puertas lógicas básicas Otras puertas lógicas Circuitos secuenciales Otros secuenciales

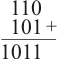
PUERTAS LÓGICAS BÁSICAS Los ordenadores trabajan con números binarios, y pueden realizar dos tipos de operaciones: Las operaciones aritméticas consisten en sumar, restar, multiplicar,... números binarios con las mismas reglas que usamos en los números decimales: Las operaciones lógicas consisten en obtener un resultado o salida que depende de la combinación de los datos de entrada. Estas operaciones se representan mediante tablas de verdad:

Estas operaciones lógicas se simbolizan como combinación de tres funciones básicas que son:

FUNCIÓN AND

La salida es un 1 únicamente cuando todas las entradas tienen valor 1:

Tabla de verdad	Simbología	Representación

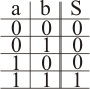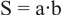FUNCIÓN OR

La salida es un 1 cuando al menos una de las entradas tiene valor 1:

Tabla de verdad	Simbología	Representación

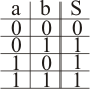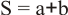FUNCIÓN NOT

Esta función, también llamada inversor, invierte el valor de la entrada:

Tabla de verdad	Simbología	Representación

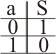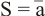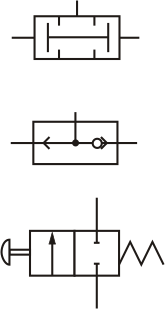
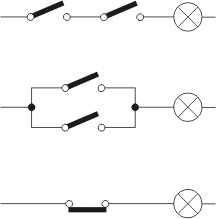
Estas funciones se realizan normalmente mediante circuitos neumáticos, eléctricos, o electrónicos:

Y asociando puertas se pueden realizar funciones complejas, de las cuales se puede expresar su función y su tabla de verdad:

OBTENCIÓN DE FUNCIONES

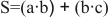
Cuando se realiza un diseño con funciones lógicas, primero se confecciona la tabla de verdad que se debe cumplir. A partir de ella se obtiene la función o expresión booleana. Para ello hay dos posibles métodos:

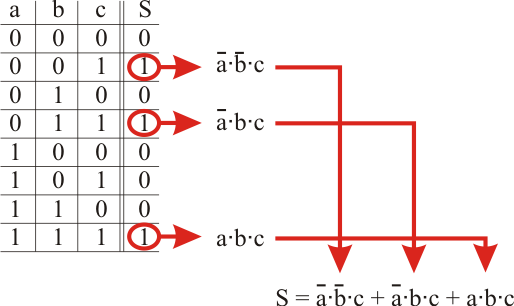
Primera forma canónica, suma de minitérminos

Se buscan las combinaciones en que la salida sea 1. En esas combinaciones se deben cumplir simultáneamente las entradas, por lo que se relacionan con una función AND, escribiendo las variables cuyo valor sea cero como negadas. Cualquiera de esas combinaciones se llama minitérmino, y cada una es igualmente válida, por lo que se pueden relacionar mediante una función OR. A la expresión obtenida se le denomina primera forma canónica.

Segunda forma canónica, producto de maxitérminos

Este procedimiento se basa en eliminar todos los casos desfavorables, por lo tanto se buscan las combinaciones en que la salida sea 0. En esas combinaciones se deben cumplir simultáneamente que las entradas sean nulas, por lo que se relacionan con una función OR, escribiendo las variables cuyo valor sea uno como negadas. Cualquiera de esas combinaciones se llama maxitérmino, y cada una debe ser eliminada, por lo que se relacionan mediante una función AND. A la expresión obtenida se le llama segunda forma canónica.

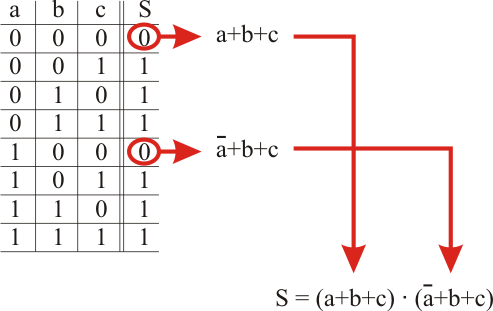
Se elegirá uno u otro método dependiendo de que sean mayoría los ceros o los unos en la tabla.

SIMPLIFICACIÓN DE FUNCIONES

El sistema formado por los elementos {0, 1} con las operaciones {+, ·, ¯} es una estructura matemática denominada álgebra, y en honor al matemático inglés George Boole, que fue el primero en definirla a mediados del siglo XIX, se llama Álgebra de Boole. Este sistema tiene una serie de propiedades, mediante las cuales se puede realizar una simplificación de las expresiones anteriormente obtenidas. Estas propiedades se pueden ver pulsando aquí.

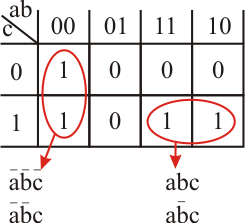
El sistema de simplificación algebráica es tedioso y dado a equívocos, por lo que se utilizan métodos más sencillos y sistemáticos, como el método de Karnaugh. Este método comienza por obtener el mapa de la función, que es una tabla en la que aparecen todas las combinaciones de la tabla de verdad:

Una vez que tenemos el mapa de Karnaugh, se realizan agrupaciones por parejas de unos. Ésto significa que en cada agrupación aparece una variable y su negación, por lo que se puede eliminar esa variable. En el ejemplo:

Y la función queda simplificada como:

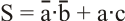
Con la fución lógica es sencillo dibujar el circuito lógico o logigrama que cumple la función. A todo el proceso de obtención de la función y dibujo del logigrama se le llama implementar la función.