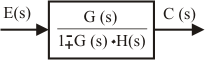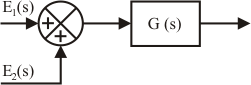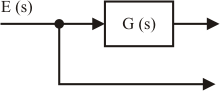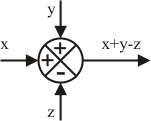
Las flechas de un diagrama indican la secuencia de operaciones y también el flujo de las señales. Cuando se utiliza una señal para más de un bloque, se usa un punto de reparto o de bifurcación, algo así como un empalme eléctrico:

Cuando hay un valor de referencia que se quiere mantener, como en el ejemplo de la velocidad de rotación del regulador de Watt, entonces se trata de una señal ficticia, y la línea de ésta se dibuja discontinua:

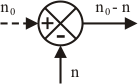
Más adelante veremos algunas ecuaciones típicas de diferentes procesos, por ahora simplemente se representarán como una letra mayúscula (normalmente G1, G2,...) que indica la función y entre paréntesis el parámetro variable del proceso, que normalmente es el tiempo, aunque también puede ser algún otro parámetro, por lo que se indica como s. Como la entrada y salida de un proceso suelen ser también funciones del mismo parámetro, el esquema del proceso será:

Con todas las ecuaciones básicas de cada proceso un sistema se puede obtener la función matemática que da la salida en función de las entradas, y las leyes de simplificación básicas son las siguientes:

Asociación de bloques en serie

La función simplificada de varios procesos en serie viene dada por el producto de las funciones parciales:

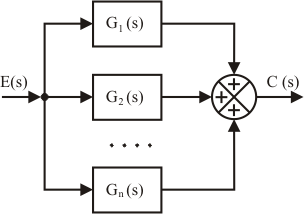
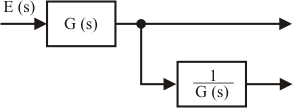
Asociación de bloques en paralelo

En este caso, la función resultante es la suma (o diferencia, según el signo en el comparador) de las distintas funciones.

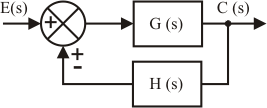
Sistemas de lazo cerrado

La función simplificada viene dada por la expresión de la derecha. El signo + o - depende del signo del comparador (hay que notar que el signo se invierte).

Otra serie de operaciones, necesarias para la simplificación de ecuaciones, se realizan mediante el desplazamiento o transposición de sumadores o de puntos de bifurcación respecto a un bloque en particular. Estas operaciones son las siguientes:

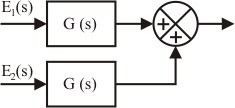
Transposición de un sumador hacia la derecha

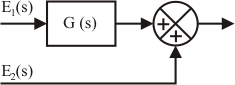
Transposición de un sumador hacia la izquierda

Y las correspondientes a los puntos de bifurcación son muy similares a las de los sumadores:

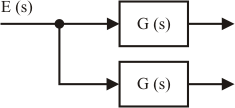
Transposición de un punto de bifurcación hacia la izquierda

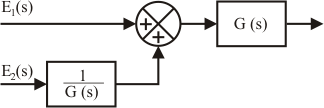
Transposición de un sumador hacia la derecha

De esta forma se puede obtener una función simplificada que no sólo sirve para tener una expresión matemática, si no que también nos puede indicar si el sistema es estable ante perturbaciones.