Definiciones
Diagramas de bloques
Función de transferencia
Sensores
Amplificadores
Actuadores |
FUNCIÓN DE TRANSFERENCIA
A la función simplificada del sistema se le da el nombre de función de transferencia del mismo:
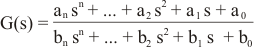
El denominador que tenga esta función recibe el nombre de ecuación característica, y es la que indica si el sistema es estable o no, tanto en la puesta en marcha como ante posibles perturbaciones. Un sistema estable recupera su salida tras un cierto tiempo después de que se produzca la perturbación:
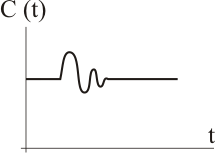
|
Para analizar la estabilidad de un sistema se analiza la ecuación característica, igualándola a cero para calcular sus raíces (valores de la variable en que la función es cero):
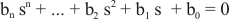
El sistema será estable si todas las raíces de su ecuación característica son negativas. Si alguna raíz es un número complejo, con parte real y parte imaginaria, la condición es que la parte real de la misma sea negativa. En ecuaciones de primer y segundo grado es sencillo obtener los ceros, pero para ecuaciones de tercer y superiores grados se utilizan métodos simplificados.
Uno de los métodos más sencillos es la factorización de la ecuación, descomponiéndola por el método de Ruffini, por ejemplo. Cuando ésto tampoco es factible, se utilizan otras formas:
El método de descarte sirve para determinar la inestabilidad del sistema, pues si a la ecuación característica le falta algún coeficiente, o los coeficientes tienen diferentes signos, al menos una de las raíces tiene parte real positiva.
Cuando ninguno de los coefeicientes del polinomio es nulo y todos tienen el mismo signo, se utiliza el método de la tabla de Routh, que es una derivación del método de Kramer de resolución de sistemas de ecuaciones, y que consiste en disponer dichos coeficientes en filas y columnas y operar con ellos:
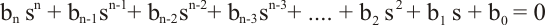
| bn |
bn-2 |
bn-4 |
... |
| bn-1 |
bn-3 |
bn-5 |
... |
| A1 |
A2 |
... |
|
| B1 |
... |
|
|
| C1 |
|
|
|
En la primera fila se escriben los coeficientes del término de mayor exponente y los que tengan la misma paridad. En la segunda fila se escriben los coeficientes de los exponentes con paridad contraria a la del primer término. En las filas siguientes, cada término se obtiene a partir de los dos que hay por encima a su derecha y los dos de la primera columna:
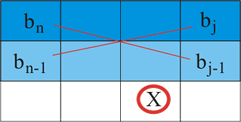 |
X = (bn-1·bj - bn·bj-1)/bn-1 |
Y así tendríamos:
A1 = (bn-1·bn-2 - bn·bn-3)/bn-1 |
A2 = (bn-1·bn-4 - bn·bn-5)/bn-1 |
... |
Para la siguiente fila tendríamos:
B1 = (A1·bn-3 - bn-1·A2)/A1 |
... |
Con este método se rellenan todas las filas hasta quedarnos con ceros, con los que no se puede operar. Saldrán tantas filas como el valor del máximo exponente, y en la última habrá un sólo término. El sistema será estable si todos los elementos de la primera columna tienen el mismo signo (las veces que cambie el signo entre los elementos indican el número de raíces positivas que tiene la ecuación).
Por ejemplo, con la ecuación característica siguiente:
s6 + 4 s5 + 3 s4 + 2 s3 + s2 + 4 s + 4
El arreglo de Routh es:
1 |
3 |
1 |
4 |
4 |
2 |
4 |
|
5/2 |
0 |
4 |
|
2 |
-12/5 |
|
|
3 |
4 |
|
|
-76/15 |
|
|
|
4 |
|
|
|
La primera columna no tiene todos sus coeficientes con
signos iguales; por lo tanto, el polinomio tiene raíces positivas, más exactamente, tiene dos.
Para saber más:
Apuntes sobre estabilidad de sistemas
![]()





